Maths 2nde Bac Pro

Préambule commun aux enseignements de mathématiques et
de physique-chimie

Intentions majeures

La classe de seconde professionnelle permet aux élèves de consolider leur maîtrise du socle commun de connaissances, de compétences et de culture afin de réussir la transition du collège vers la voie professionnelle. Elle les prépare au cycle terminal dans l’objectif d’une insertion professionnelle ou d’une poursuite d’études supérieures réussie.
L’enseignement de mathématiques et de physique-chimie en classe de seconde professionnelle concourt à la formation intellectuelle, professionnelle et civique des élèves.

Le programme est conçu à partir des intentions suivantes :

• permettre à tous les élèves de consolider leurs acquis du collège ;
• former les élèves à l’activité mathématique et scientifique en poursuivant la pratique des démarches mathématique et scientifique commencées au collège ;
• fournir aux élèves des outils mathématiques et scientifiques utiles pour les enseignements généraux et professionnels ;
• assurer les bases mathématiques et scientifiques nécessaires à une poursuite d’études et à la formation tout au long de la vie ;
• participer au développement de compétences transversales qui contribuent à l’insertion sociale et professionnelle des élèves et qui leur permettent de devenir des citoyens éclairés et des professionnels capables de s’adapter à l’évolution des métiers liée à la transformation digitale ;
• contribuer à donner une culture scientifique et civique indispensable à une époque où la technologie et le numérique font partie intégrante de la vie quotidienne.

Compétences travaillées

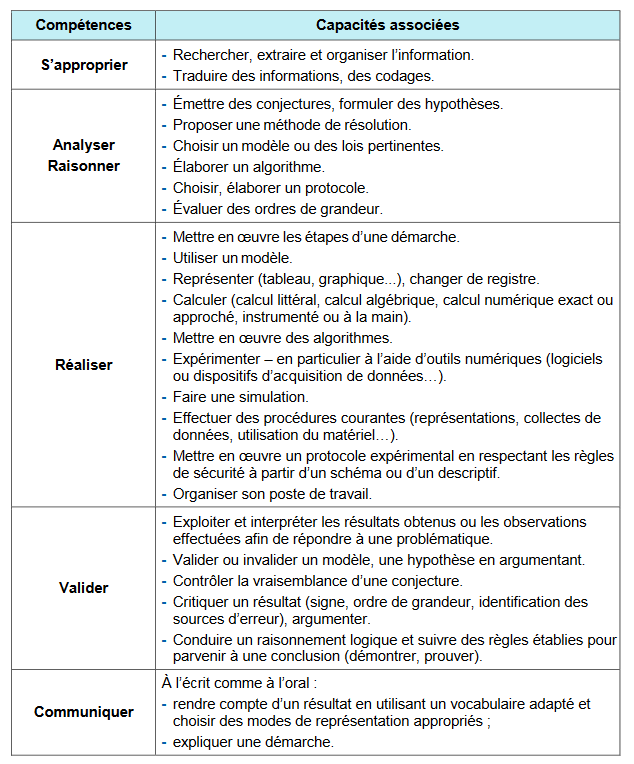
Dans le prolongement des enseignements dispensés à l’école primaire et au collège, cinq compétences communes aux mathématiques et à la physique-chimie sont travaillées. Elles permettent de structurer la formation et l’évaluation des élèves. L’ordre de leur présentation ne prescrit pas celui dans lequel ces compétences seront mobilisées par l’élève dans le cadre d’activités. Une liste de capacités associées à chacune des compétences indique la façon dont ces dernières sont mises en œuvre. Le niveau de maîtrise de ces compétences dépend de l’autonomie et de l’initiative requises dans les activités proposées aux élèves.

Programme de mathématiques

Dans la continuité du collège, le programme de mathématiques de la classe de seconde professionnelle vise à développer la démarche mathématique à travers la résolution de problèmes. À partir de visualisations, d’expérimentations, d’essais et/ou de simulations informatiques, des conjectures sont émises et sont validées ou invalidées par le calcul et le raisonnement avant une formalisation des réponses au problème. L’environnement numérique se révèle incontournable dans cette démarche et l’utilisation des outils numériques trouve naturellement sa place dans cet enseignement.

Les problèmes rencontrés peuvent être de natures différentes : réinvestissement de connaissances déjà travaillées, acquisition d’une nouvelle connaissance ou construction d’une nouvelle capacité, activité de recherche. La démarche mathématique s’appuie sur cinq compétences qui sont explicitées dans le tableau des compétences travaillées présent dans le préambule commun aux programmes de mathématiques et de physique-chimie.

La résolution de problèmes et l’algorithmique, présentes dans tous les domaines des mathématiques, permettent aux élèves de s’exprimer, d’échanger, de communiquer, d’interagir, d’acquérir une autonomie de jugement et de pensée, tout en développant leur créativité et leur esprit d’initiative. La résolution de problèmes offre aussi la possibilité d’une coopération entre élèves, tant dans le cadre habituel que dans celui de la co-intervention.

Les mathématiques contribuent à la construction de compétences transversales par les différents domaines qu’elles abordent, par exemple :

• la géométrie, qu’elle soit plane ou dans l’espace, contribue largement à développer diverses formes de raisonnement, en particulier le raisonnement déductif, et à modéliser des situations concrètes afin d’interpréter objectivement la réalité ;
• la maîtrise de la proportionnalité dans divers contextes, la compréhension notamment des pourcentages, des échelles, de la notion de vitesse, participe à la construction de
• la capacité à traiter l’information, tout en développant l’esprit critique.

Les compétences d’expression orale et écrite, à la fois usuelles et spécifiques, sont également développées au travers d’activités nécessitant :

• d’être capable de lire des textes, des schémas, des représentations d’objets de l’espace en 2D ;
• de prendre des initiatives en mobilisant et en articulant ses connaissances et capacités ;
• de faire preuve d’esprit critique par la validation des résultats ;
• d’expliquer la démarche et de communiquer les résultats obtenus à l’oral ou à l’écrit.

Organisation du programme

Le programme de mathématiques est constitué des domaines de connaissances suivants :

• statistique et probabilités ;
• algèbre – analyse ;
• géométrie.

Le domaine Statistique et probabilités se compose de deux modules.

Le domaine Algèbre – Analyse se compose de trois modules.

Le module Calculs commerciaux et financiers ne concerne que les spécialités de baccalauréat professionnel ne comportant pas d’enseignement de physique-chimie.

Le domaine Géométrie se compose d’un seul module.

En complément de ces domaines de connaissances, trois modules sont abordés : Automatismes, Algorithmique et programmation et Vocabulaire ensembliste et logique. Ces modules ne doivent pas faire l’objet de cours spécifiques, mais doivent être travaillés lors de l’étude des différents domaines du programme.

Pour chaque module sont indiqués :

• les objectifs ;
• les liens avec le cycle 4 ;
• les capacités et connaissances exigibles ;
• des exemples d’algorithmes ou d’activités numériques.

Certains modules comportent des commentaires qui précisent entre autres les limites du programme et des approfondissements possibles.

Les domaines du programme de physique-chimie qui nécessitent la mise en œuvre de capacités et connaissances de mathématiques sont indiqués à la fin des modules concernés afin de garantir la cohérence de la formation scientifique.

Statistique et probabilités

Ce domaine constitue un enjeu essentiel de formation et favorise les liaisons avec les autres enseignements. Il s’agit de fournir aux élèves des outils pour comprendre le monde, pour décider et agir dans la vie quotidienne.
Les objectifs principaux de ce domaine sont :

• identifier, classer, hiérarchiser l’information ;
• exploiter et représenter des données ;
• interpréter un résultat statistique ;
• étudier des situations simples relevant des probabilités.

Le calcul d’indicateurs, la construction et l’interprétation de graphiques ainsi que la simulation d’expériences aléatoires à l’aide d’outils numériques sont des passages obligés de la formation.

Statistiques à une variable

Objectifs

L’objectif de ce module est de favoriser la prise d’initiative et la conduite de raisonnements pour interpréter, analyser ou comparer des séries statistiques. Pour ce faire, on s’appuie sur des situations concrètes liées aux spécialités professionnelles ou issues de la vie courante. Des données réelles sont à privilégier. L’utilisation des outils numériques est nécessaire. Ce
module est particulièrement propice aux changements de registres (textes, tableaux, graphiques) qui participent au renforcement de la maîtrise de la langue.

Liens avec le cycle 4

Au cycle 4, les élèves ont appris à recueillir, organiser, interpréter, représenter et traiter des données, à utiliser un tableur-grapheur pour présenter des données sous la forme d’un tableau ou d’un diagramme. Ils ont également appris à calculer des effectifs et des fréquences, à calculer et à interpréter des indicateurs de position et de dispersion d’une série statistique. Ils ont étudié moyenne, médiane et étendue.
En seconde, ils consolident ces notions et découvrent d’autres représentations et indicateurs permettant de comparer des séries statistiques. Ils découvrent la notion d’intervalle comme ensemble de nombres vérifiant des inégalités.

Capacités et connaissances

Capacités	Connaissances
Recueillir et organiser des données statistiques.	Regroupement par classes d’une série statistique.
Organiser des données statistiques en choisissant un mode de représentation adapté à l’aide des fonctions statistiques d’une calculatrice ou d’un tableur. Extraire des informations d’une représentation d’une série statistique.	Représentation d’une série statistique par un diagramme en secteurs, en bâtons, en colonnes, à lignes brisées
Comparer et interpréter des séries statistiques à l’aide d’indicateurs de position et de dispersion calculés avec les fonctions statistiques d’une calculatrice ou d’un tableur.	Indicateurs de position : mode, classe modale, moyenne, médiane, quartiles. Indicateurs de dispersion : étendue, écart type, écart interquartile Q3 – Q1.
Construire le diagramme en boîte à moustaches associé à une série statistique avec ou sans TIC. Comparer et interpréter des diagrammes en boîte à moustaches.	Diagrammes en boîte à moustaches.

Fluctuations d’une fréquence selon les échantillons, probabilités

Objectifs

L’objectif de ce module est de formaliser les notions élémentaires de probabilités abordées au cycle 4 et de faire percevoir la loi des grands nombres de manière expérimentale. Il se traite en prenant appui sur des situations concrètes, issues de la vie courante ou du domaine professionnel. La compréhension et l’acquisition des concepts sont facilitées par l’expérimentation réalisée à l’aide de simulations informatiques. L’ensemble des issues est fini.

Liens avec le cycle 4

Au cycle 4, les élèves ont découvert le vocabulaire relatif aux probabilités. Ils ont abordé les questions relatives au hasard et sont capables de calculer des probabilités dans des cas simples. Ils ont exprimé des probabilités sous diverses formes (décimale, fractionnaire, pourcentage) et fait le lien entre fréquences et probabilité, en constatant le phénomène de stabilisation des fréquences. En seconde, les élèves réinvestissent ces notions et découvrent les arbres de dénombrement.

Capacités et connaissances

Capacités	Connaissances
Expérimenter pour observer la fluctuation des fréquences (jets de dés, lancers de pièces de monnaie…). Réaliser une simulation informatique, dans des cas simples, permettant la prise d’échantillons aléatoires de taille n fixée, extraits d’une population où la fréquence p relative à un caractère est connue. Déterminer l’étendue des fréquences, relatives à un caractère, de la série d’échantillons de taille n obtenus par expérience concrète ou simulation	Vocabulaire des probabilités : expérience aléatoire, ensemble des issues (univers), événement, probabilité. Expérience aléatoire à deux issues. Échantillon aléatoire de taille n pour une expérience à deux issues (avec remise). Notion de tirage au hasard et avec remise de n éléments dans une population où la fréquence p relative à un caractère est connue. Fluctuation d’une fréquence relative à un caractère, sur des échantillons de taille n fixée
Estimer la probabilité d’un événement à partir des fréquences.	Stabilisation relative des fréquences vers la probabilité de l’événement quand n augmente
Calculer la probabilité d’un événement dans le cas d’une situation aléatoire simple. Faire preuve d’esprit critique face à une situation aléatoire simple.	Dénombrements à l’aide de tableaux à double entrée ou d’arbres.

Algèbre -Analyse

Ce domaine permet de former les élèves à la démarche de résolution de problèmes et de les faire progresser dans la maîtrise du calcul numérique et algébrique. Il met en évidence les liens entre les différents registres (numérique, algébrique, graphique) des fonctions utilisées. Les situations choisies permettent d’approcher les grands débats de société, par exemple autour du développement durable, et de traiter des problématiques parfaitement identifiées. Elles sont, autant que possible, adaptées aux métiers préparés afin de donner du sens aux notions étudiées.
Les objectifs principaux de ce domaine sont :

• modéliser une situation ;
• résoudre des problèmes du premier degré en choisissant une méthode adaptée ;
• découvrir et étudier de nouvelles fonctions

L’étude des fonctions est facilitée par l’utilisation de tableurs et de logiciels de géométrie dynamique. L’utilisation des calculatrices et de l’outil informatique pour pallier les difficultés liées aux calculs algébriques, résoudre des équations, inéquations ou systèmes d’équations, construire ou interpréter des courbes, sont des passages obligés de la formation.
La notion d’intervalle, présentée comme ensemble de nombres vérifiant des inégalités, est nouvelle. Elle est introduite lors du module Résolution d’un problème du premier degré ou du module Fonctions.

Résolution d’un problème du premier degré

Objectifs

L’objectif principal de ce module est de traduire un problème par une équation ou une inéquation du premier degré, de l’étudier et de le résoudre.

Liens avec le cycle 4

Au cycle 4, les élèves ont appris à :

• utiliser le calcul littéral ;
• mettre un problème en équation en vue de sa résolution ;
• résoudre algébriquement des équations du premier degré ou s’y ramenant (équations produits), en particulier des équations du type x2 = a.

En seconde, les élèves approfondissent ces notions. Ils découvrent les inéquations du premier degré à une inconnue. La résolution des équations du type ax = b permet de réinvestir et de consolider le traitement algébrique de problèmes modélisant une situation de proportionnalité.

Capacités et connaissances

Capacités	Connaissances
Traduire un problème par une équation ou une inéquation du premier degré à une inconnue. Résoudre algébriquement, graphiquement sans ou avec outils numériques (grapheur, solveur, tableur) : une équation du premier degré à une inconnue ; une inéquation du premier degré à une inconnue. Choisir et mettre en œuvre une méthode de résolution adaptée au problème.	Équation du premier degré à une inconnue. Inéquation du premier degré à une inconnue. Intervalles de ℝ

Fonctions

Objectifs

Les objectifs de ce module sont :

• consolider et réinvestir les connaissances sur la notion de fonction abordées au collège au travers de situations issues des autres disciplines, de la vie courante ou professionnelle ;
• exploiter différents registres, notamment le registre algébrique, le registre graphique et le passage de l’un à l’autre ;
• étudier quelques fonctions de référence afin de se constituer un répertoire d’images mentales de leurs courbes représentatives sur lesquelles s’appuyer lors de l’étude de fonctions générées à partir de celles-ci ;
• introduire l’étude des variations d’une fonction et les notions liées aux extremums ;
• modéliser des problèmes issus de situations concrètes à l’aide de fonctions afin de les résoudre.

Le vocabulaire élémentaire sur les fonctions est abordé en situation. Les fonctions définies sur un intervalle de ℝ permettent de modéliser des phénomènes continus. On ne se limite pas aux intervalles du type [a ; b], avec a et b réels ; en fonction des situations étudiées, les élèves peuvent être confrontés à d’autres types d’intervalles (]a ; b[, [a ; b[, ]a ; b], avec a et b réels). Les modèles mathématiques obtenus peuvent conduire à l’étude de fonctions sur ℝ. On peut également confronter les élèves à des exemples de fonctions définies sur ℕ pour modéliser des phénomènes discrets. Pour la modélisation de phénomènes physiques, le nom de la variable peut être choisi en cohérence avec la situation, par exemple la variable t pour le temps.Les outils numériques (logiciel de géométrie dynamique, calculatrice, tableur ou logiciel de programmation) sont mis à profit pour obtenir la courbe représentative d’une fonction et pour établir un tableau de valeurs.

Liens avec le cycle 4

Au cycle 4, les élèves ont appris à :

• manipuler la notion de fonction ;
• passer d’un mode de représentation d’une fonction à un autre ;
• déterminer, à partir d’un mode de représentation, l’image ou un antécédent d’un nombre par une fonction ;
• représenter graphiquement une fonction linéaire, une fonction affine ;
• modéliser une situation de proportionnalité à l’aide d’une fonction linéaire ;
• modéliser un phénomène continu par une fonction ;
• résoudre des problèmes modélisés par des fonctions ;
• résoudre algébriquement des équations du premier degré ou s’y ramenant (équations produits), en particulier des équations du type x2 = a.

En seconde, les élèves consolident les notions de fonction, de variable et découvrent la notion d’équation d’une courbe représentative d’une fonction.
À partir de la courbe représentative d’une fonction ƒ, ils apprennent à établir un tableau de variations d’une fonction et à obtenir la courbe représentative de la fonction qui à x associe ƒ(x) + k, où k est un réel donné.
Ils découvrent la fonction carré comme nouvelle fonction de référence et déduisent de sa courbe représentative, l’allure de celle de la fonction qui à x associe kx2, où k est un réel donné.
Ils déduisent, des variations d’une fonction ƒ, celles de la fonction kƒ, où k est un réel donné.

Ils apprennent à résoudre des équations du type ƒ(x) = c, ou des inéquations du type ƒ(x) < c, où c est un réel donné.
Les systèmes de deux équations du premier degré à deux inconnues sont introduits dans ce module. Leur résolution se fait graphiquement, à l’aide d’outils numériques.

Capacités et connaissances

Capacités	Connaissances
Exploiter différents modes de représentation d’une fonction et passer de l’un à l’autre (expression, tableau de valeurs, courbe représentative). Selon le mode de représentation : identifier la variable ; déterminer l’image ou des antécédents éventuels d’un nombre par une fonction définie sur un ensemble donné. Reconnaître une situation de proportionnalité et déterminer la fonction linéaire qui la modélise.	Différents modes de représentation d’une fonction (expression, tableau de valeurs, courbe représentative). Variable, fonction, image, antécédent et notation ƒ(x).Intervalles de ℝ.Fonctions linéaires.
Relier courbe représentative et tableau de variations d’une fonction. Déterminer graphiquement les extremums d’une fonction sur un intervalle	Fonction croissante ou décroissante sur un intervalle. Tableau de variations. Maximum, minimum d’une fonction sur un intervalle.
Exploiter l’équation y = ƒ(x) d’une courbe : vérifier l’appartenance d’un point à une courbe ; calculer les coordonnées d’un point de la courbe.	Courbe représentative d’une fonction ƒ : la courbe d’équation y = ƒ(x) est l’ensemble des points du plan dont les coordonnées (x;y) vérifient y = ƒ(x).
Représenter graphiquement une fonction affine. Déterminer l’expression d’une fonction affine à partir de la donnée de deux nombres et de leurs images. Déterminer graphiquement le coefficient directeur d’une droite non verticale. Faire le lien entre coefficient directeur et pente dans un repère orthonormé. Reconnaître que deux droites d’équations données sont parallèles. Résoudre graphiquement, ou à l’aide d’outils numériques, un système de deux équations du premier degré à deux inconnues. Construire la parabole représentant la fonction carré et donner son tableau de variations.	Fonction affine :- courbe représentative ;- coefficient directeur et ordonnée à l’origine d’une droite représentant une fonction affine ;- équation réduite d’une droite ;- sens de variation en fonction du coefficient directeur de la droite qui la représente.Interprétation du coefficient directeur de la droite représentative d’une fonction affine comme taux d’accroissement.Système de deux équations du premier degré à deux inconnues.Courbe représentative de la fonction carré.Sens de variation de la fonction carré.
Déduire de la courbe représentative d’une fonction ƒ sur un intervalle donné celle de la fonction qui à x associe ƒ(x) + k, où k est un nombre réel donné, sur le même intervalle. Déduire de la courbe représentative de la fonction carré, l’allure de celle de la fonction définie par ƒ(x) = kx2, où k est un nombre réel donné. Déduire des variations d’une fonction ƒ sur un intervalle donné celles de la fonction kƒ, où k est un nombre réel donné, sur le même intervalle.
Dans le cadre de problèmes modélisés par des fonctions, résoudre par une méthode algébrique ou graphique une équation du type ƒ(x) = c ou une inéquation du type ƒ(x) < c, où c est un réel donné et ƒ une fonction affine ou une fonction du type x ↦ kx2 (avec k réel donné).	Résolution algébrique ou graphique.

Calculs commerciaux et financiers (uniquement pour les spécialités de baccalauréat professionnel ne comportant pas d’enseignement de physique-chimie)

Objectifs

Ce module permet de renforcer la maîtrise des pourcentages communément utilisés dans les organisations (entreprises commerciales, associations, établissements publics) lors de l’établissement ou de l’utilisation de divers documents (factures, bulletins de paye, documents financiers…). Ce module se prête à des séances de co-intervention, par exemple lors de l’utilisation de logiciels métiers.

Capacités et connaissances

Capacités	Connaissances
Compléter une facture, un bon de commande, réaliser un devis en déterminant dans le cadre de situations professionnelles : un prix ; un coût ; une marge ; une taxe ; une réduction commerciale (remise, rabais, ristourne) ; un taux.	Pourcentages. Coefficients multiplicateurs.
Calculer le montant : d’un intérêt simple ; d’une valeur acquise. Déterminer graphiquement ou par le calcul : un taux annuel de placement ; la durée de placement (exprimée en jours, quinzaines, mois ou années) ; le montant du capital placé.	Capital, taux, intérêt, valeur acquise.

Géométrie

Ce domaine vise à mobiliser les configurations du plan et les connaissances sur les solides de l’espace déjà étudiés au collège dans le but de résoudre des problèmes, de développer la vision dans l’espace et de réactiver les propriétés de géométrie plane.
L’utilisation des théorèmes de géométrie et des formules de calcul de longueurs, d’aires et de volumes permet de remobiliser les connaissances sur les quotients, les racines carrées, les valeurs exactes, les valeurs arrondies en situation.
La géométrie développe des capacités de représentation et il importe de s’appuyer sur des figures réalisées selon des modalités diverses (tracé à main levée ou avec des instruments, figure codée, utilisation de logiciels).
Dans le cadre de la résolution de problèmes, l’utilisation d’un logiciel de géométrie dynamique permet d’observer ou de conjecturer des propriétés, de visualiser des résultats, dans le plan ou dans l’espace, et facilite la prise d’initiatives et l’autonomie de l’élève.

Liens avec le cycle 4

Au cycle 4, les élèves ont appris à :

•  calculer avec des grandeurs mesurables ; exprimer les résultats dans les unités adaptées ;
•  mobiliser les connaissances des figures, des configurations au programme pour déterminer des grandeurs géométriques ;
•  utiliser un logiciel de géométrie dynamique pour représenter des figures ou des solides.

En seconde, ce module permet de consolider et d’approfondir les capacités et connaissances travaillées au cycle 4.

Capacités et connaissances

Capacités	Connaissances
Reconnaître, nommer un solide usuel. Nommer les solides usuels constituant d’autres solides. Calculer des longueurs, des mesures d’angles, des aires et des volumes dans les figures ou solides (les formules pour la pyramide, le cône et la boule sont fournies).	Solides usuels : le cube, le pavé droit, la pyramide, le cylindre droit, le cône, la boule.Figures planes usuelles : triangle, quadrilatère, cercle.Le théorème de Pythagore et sa réciproque. Le théorème de Thalès dans le triangle.Formule donnant le périmètre d’un cercle.Somme des mesures, en degré, des angles d’un triangle.Formule de l’aire d’un triangle, d’un carré, d’un rectangle, d’un disque.Formule du volume du cube, du pavé droit et du cylindre.
Déterminer les effets d’un agrandissement ou d’une réduction sur les longueurs, les aires et les volumes.	Grandeurs proportionnelles.